|
|
|
A theory of stereo image formation is presented that enables a complete classification of all possible stereo views, including non-perspective varieties. Towards this end, the notion of epipolar geometry is generalized to apply to multiperspective images. It is shown that any stereo pair must consist of rays lying on one of three varieties of quadric surfaces. A unified representation is developed to model all classes of stereo views, based on the concept of a quadric view. The benefits include a unified treatment of projection and triangulation operations for all stereo views. The framework is applied to derive new types of stereo image representations with unusual and useful properties. Experimental examples of these images are constructed and used to obtain 3D binocular object reconstructions.
In particular, we present results on two new types of stereo representations, stereo cyclograph and pushbroom panorama.
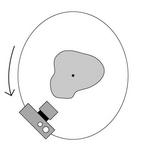
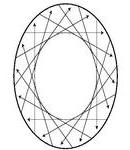
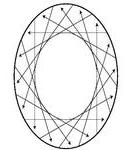
A stereo cyclograph is generated by moving an inward-looking camera on an ellipse (1a) and stacking the sequence of images into an x-y-theta volume (1b). y-theta slices of the volume form cyclograph images. All of the rays in each cyclograph are tangent to a sheared cylinder (each cross section is an ellipse). A stereo cyclograph pair consists of two views that are both tangent to the same sheared cylinder, but with tangent rays oriented in opposite directions (1c-d).
| 
| 
| 
|
| (a) | (b) | (c) | (d) |
| Figure 1. Geometry of stereo cyclographs | |||
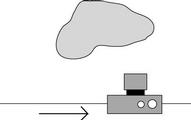
A pushbroom panorama is generated by translating a camera parallel to the image plane u-axis (2a), and placing column i of pixels from every input image into successive columns of a new image Ii. Any two pushbroom panoramas Ii and Ij form a stereo pair with rays lying on a pencil of epipolar planes (2b).
| 
|
| (a) | (b) |
| Figure 2. Geometry of pushbroom panoramas | |
|
|
|
| Toy horse | Cereal box | Human face |
|
|
|
| Outdoor #1 | Outdoor #2 | Indoor |