Fourier Analysis of the 2D Screened Poisson Equation
for Gradient Domain Problems

 

Pravin Bhat, Brian Curless, Michael Cohen, C. Lawrence Zitnick

 

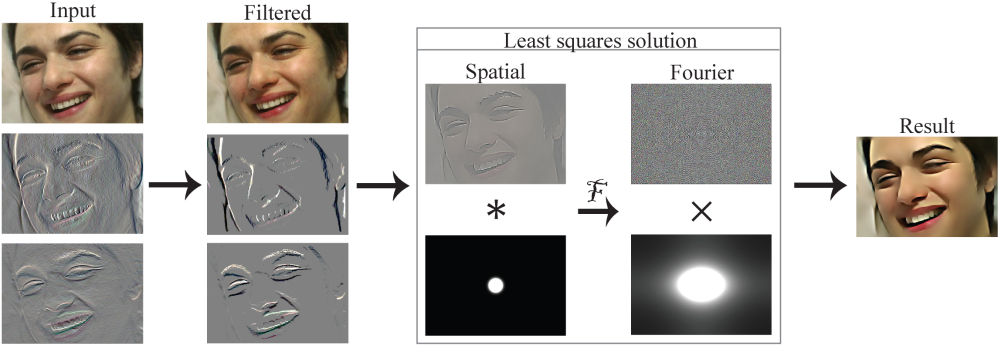
Abstract

We analyze the problem of reconstructing a 2D function that approximates a set of desired gradients and a data term. The combined data and gradient terms enable operations like modifying the gradients of an image while staying close to the original image. Starting with a variational formulation, we arrive at the 'screened Poisson equation' known in physics. Analysis of this equation in the Fourier domain leads to a direct, exact, and efficient solution to the problem. Further analysis reveals the structure of the spatial filters that solve the 2D screened Poisson equation and shows gradient scaling to be a well-defined sharpen filter that generalizes Laplacian sharpening, which itself can be mapped to gradient domain filtering. Results using a DCT-based screened Poisson solver are demonstrated on several applications including image blending for panoramas, image sharpening, and de-blocking of compressed images.

 

image001.jpg

 

 

Citation

 

  • Bhat P., Curless B., Cohen M., and Zitnick L. Fourier Analysis of the 2D Screened Poisson Equation for Gradient Domain Problems. European Conference on Computer Vision (ECCV) 2008.
  • Bibtex

 

 

Downloads

 

  • ECCV Paper - (PDF)
  • ECCV Poster - (PDF)
  • Code for the Fourier solver - (CPP)

 

 

Related projects