Abstract
This paper introduces an alternative approach to sampling from autoregressive models. Autoregressive models are typically sampled sequentially, according to the transition dynamics defined by the model. Instead, we propose a sampling procedure that initializes a sequence with white noise and follows a Markov chain defined by Langevin dynamics on the global log-likelihood of the sequence. This approach parallelizes the sampling process and generalizes to conditional sampling, using an autoregressive model as a Bayesian prior. This allows us to steer the output of a generative model using a conditional likelihood or constraints. We apply these techniques to autoregressive models in the visual and audio domains, with competitive results for audio source separation, super-resolution, and inpainting.

Audio Demos + Comparisons
We present audio demos that show the quality of samples generated with PnF. We also compare with task specific baselines when applicable
Spectrogram Conditioned Generation
We show that PnF sampling is indistinguishable from autoregressive sampling and can faithfully reproduce the ground truth.
Voice
|
|
|
|
| GT |
Autoregressive Wavenet |
PnF Wavenet - 2048 iterations |
Piano
|
|
|
|
| GT |
Autoregressive Wavenet |
PnF Wavenet - 2048 iterations |
Varying Number of Iterations
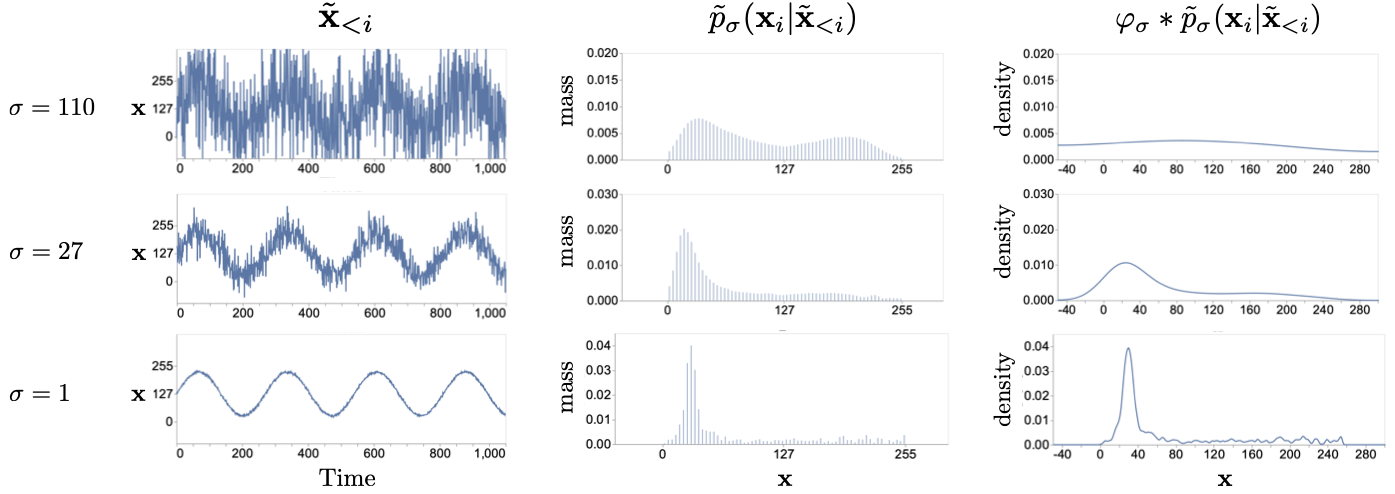
The quality of samples from our method is dependent on the number of Langevin iterations at each noise level. We show this effect below.
|
|
|
|
|
| PnF Wavenet - 64 iterations |
PnF Wavenet - 128 iterations |
PnF Wavenet - 512 iterations |
PnF Wavenet - 2048 iterations |
Audio Super-Resolution: Piano
4x Super-Resolution
|
|
|
|
|
| Input (4x Downsampled) |
PnF (WaveNet) Upsampled |
Spline |
KEE Network [1] |
8x Super-Resolution
|
|
|
|
|
| Input (8x Downsampled) |
PnF (WaveNet) Upsampled |
Spline |
KEE Network [1] |
16x Super-Resolution
|
|
|
|
|
| Input (16x Downsampled) |
PnF (WaveNet) Upsampled |
Spline |
KEE Network [1] |
32x Super-Resolution
|
|
|
| Input (32x Downsampled) |
PnF (WaveNet) Upsampled |
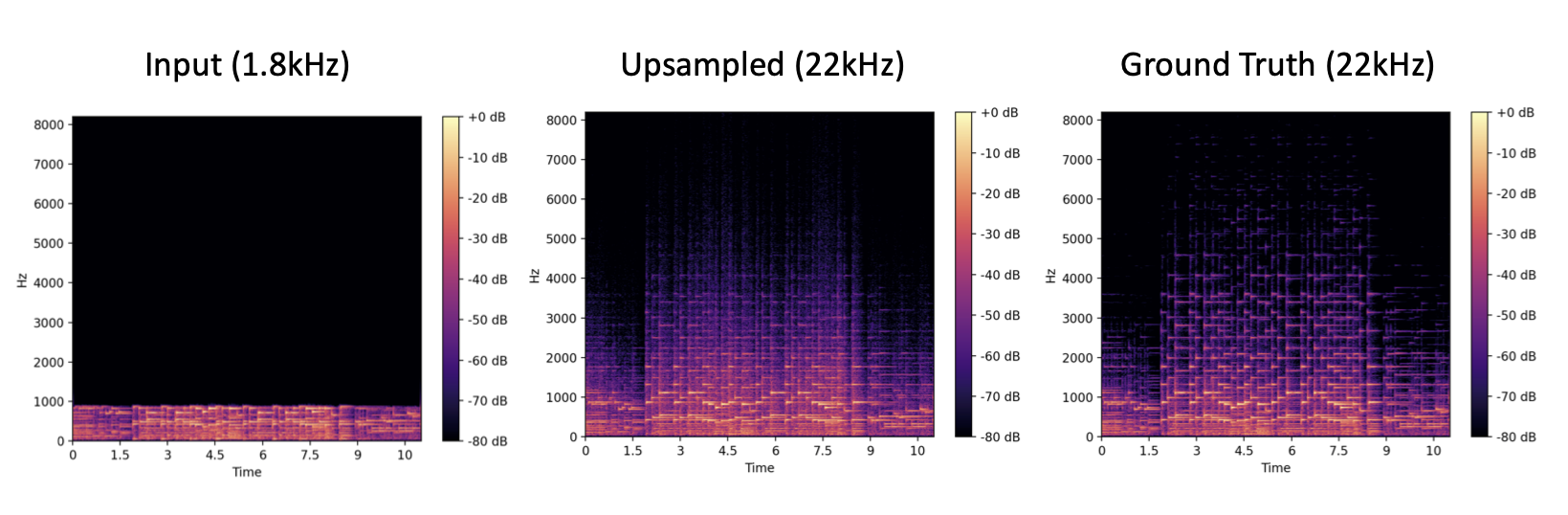
Sample spectrograms showing the effect of 12x super-resolution. This example is from the top of the page
[1] Kuleshov, V., Enam, S. Z., and Ermon, S. Audio super-resolution using neural nets. ICLR (Workshop Track), 2017.
Audio Super-Resolution: Voice
4x Super-Resolution
|
|
|
|
|
| Input (4x Downsampled) |
PnF (WaveNet) Upsampled |
Spline |
KEE Network [1] |
8x Super-Resolution
|
|
|
|
|
| Input (8x Downsampled) |
PnF (WaveNet) Upsampled |
Spline |
KEE Network [1] |
16x Super-Resolution
|
|
|
|
|
| Input (16x Downsampled) |
PnF (WaveNet) Upsampled |
Spline |
KEE Network [1] |
Source Separation
|
|
|
|
|
|
|
|
|
|
| GT |
PnF (WaveNet) |
Conv-TasNet [2] |
Demucs [3] |
[2] Luo, Y. and Mesgarani, N. Conv-tasnet: Surpassing idealtime–frequency magnitude masking for speech separa-tion.IEEE/ACM Transactions on Audio, Speech, andLanguage Processing, 2019.
[3] Defossez, A., Usunier, N., Bottou, L., and Bach, F. Musicsource separation in the waveform domain
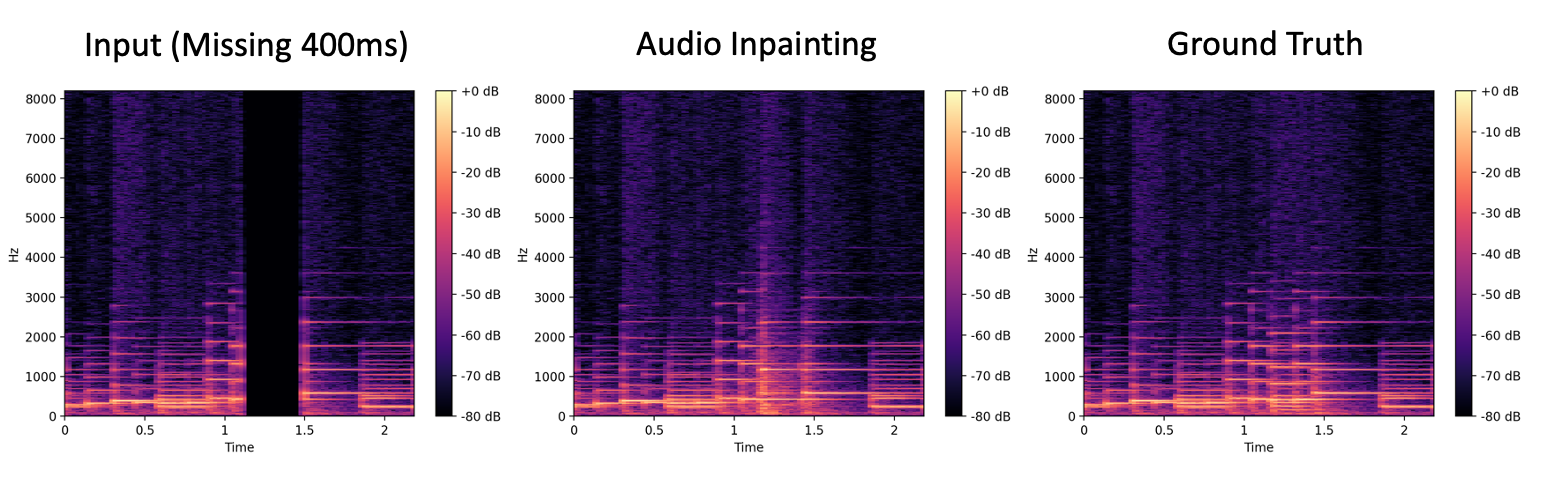
Audio Inpainting
Piano
|
|
|
|
|
|
| Ground Truth |
Input (Missing 200ms) |
PnF (WaveNet) Inpainted |
Input (Missing 400ms) |
PnF (WaveNet) Inpainted |
Voice
|
|
|
|
|
|
| Ground Truth |
Input (Missing 100ms) |
PnF (WaveNet) Inpainted |
Input (Missing 200ms) |
PnF (WaveNet) Inpainted |
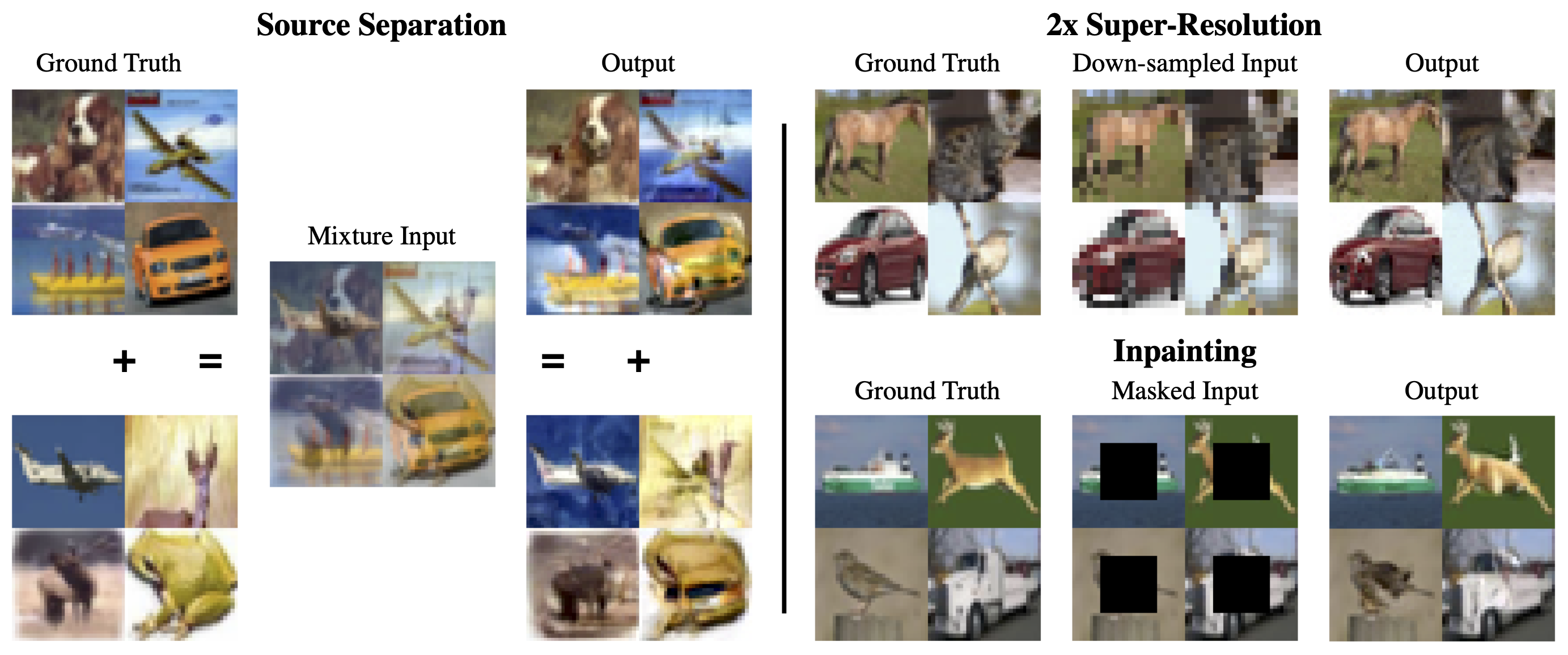
We show results using PnF to sample from a PixelCNN++ model on the CIFAR10 dataset. We show results for three different tasks: source separation (left), 2x super-resolution (top right), and inpainting (bottom right)
Keywords: Source Separation with Generative Models. Source Separation with Wavenet. Wavenet for Source Separation. Audio Super Resolution with Generative Models. Audio Super Resolution with Wavenet. Wavenet for Audio Super Resolution. Wavenet for Audio Inpainting. Audio Inpainting with Generative Models.